Logistics là một ngành có truyền thống lâu đời và có tác động trực tiếp tới hiệu quả hoạt động của nhiều ngành kinh doanh. Từ trước đến nay, ngành này vẫn hoạt động trên cơ sở kinh nghiệm của con người với những cách thức tính toán tương đối thủ công, ít hiệu quả, mất thời gian, tốn nhân công và chi phí không cần thiết. Những bài toán vận hành tồn tại trong ngành cũng là những bài toán phức tạp. Để có thể giải quyết những bài toán này một cách hiệu quả, thì cách thức thủ công không phải là một cách tiếp cận nên làm.
Nếu từng làm việc trong lĩnh vực logistics, chuỗi cung ứng hoặc học tập, nghiên cứu về toán học, thuật toán, chắc hẳn bạn đã ít nhất một lần nghe về cụm “Vehicle Routing Problem (VRP - Vấn đề Hoạch định Tuyến đường)”. Vehicle Routing Problem là một vấn đề toán học, và đề bài gốc của bài toán này gói gọn trong câu hỏi:

1. Bài toán Vehicle Routing Problem - Chúng ta đã gặp ở đâu?

Thực chất, bài toán Vehicle Routing Problem (VRP - Vấn đề Hoạch định Tuyến đường) luôn xuất hiện trong đời sống thường ngày chứ không chỉ trong khía cạnh kinh doanh. Giả dụ như với một nhân viên văn phòng, bài toán Vehicle Routing Problem có thể diễn ra như sau: Đâu là tuyến đường nhanh nhất để xuất phát từ nhà (điểm xuất phát) đến công ty, sau đó là qua ngân hàng để đăng ký mở thẻ tín dụng mới, tiếp theo là đến trường học để đón con, rồi tạt qua chợ để mua đồ ăn cho buổi tối, cuối cùng là quay về nhà, tức quay lại điểm xuất phát.
Vấn đề sẽ trở nên khó nhằn khi ta đưa bài toán trên vào một tình huống khác - khi người cần giải quyết bài toán không còn là nhân viên văn phòng đã đi làm lâu năm - mà là một bạn sinh viên mới lên thành phố để vào đại học.

Hãy tưởng tượng tình huống giả định mới như sau: Nam - bạn sinh viên năm đầu đại học này muốn kiếm một công việc làm thêm để trang trải và công việc cậu bạn chọn là làm shipper giao bánh mì. Hôm nay là ngày làm việc đầu tiên của Nam. Vào 7h30 sáng, Nam nhận chuyến giao bánh đầu tiên cho các nhân viên văn phòng. Chuyến hàng của cậu có 10 đơn hàng, và cần giao tới 10 tòa nhà văn phòng khác nhau.
Đâu sẽ là lời giải tối ưu cho bài toán trên, khi mà đây là ngày đầu tiên Nam làm shipper tại một thành phố xa lạ? Sử dụng Google Maps cho từng điểm giao? Hỏi đàn anh? Hay đơn giản là đi bừa từng điểm?
Tiếp theo ở phần hai của bài viết, Abivin sẽ nhìn vào khía cạnh toán học, đi qua ngắn gọn lịch sử của bài toán, đặc điểm của bài toán trong toán học và nghiên cứu, cũng như cách các nhà nghiên cứu giải quyết bài toán này.
*Lưu ý: Nếu bạn đọc muốn đi ngay vào cách giải quyết bài toán Vehicle Routing Problem trong thực tiễn doanh nghiệp, hãy đọc thẳng phần ba của bài viết.
2. Vehicle Routing Problem trong toán học và nghiên cứu
a. Lịch sử của Vehicle Routing Problem

Vehicle Routing Problem bắt nguồn từ năm 1959 khi George Dantzig và John Ramser thiết lập công thức toán học và phương pháp tiếp cận bằng thuật toán để giải quyết vấn đề cung cấp xăng dầu cho các trạm dịch vụ. Thông thường trong bài toán này, hàng hóa được đặt tại kho để mang đi giao cho những khách hàng đã đặt hàng. Mục tiêu của VRP là giảm thiểu tổng chi phí tuyến đường. Năm 1964, Clarke và Wright đã cải tiến cách giải của Dantzig và Ramser bằng cách sử dụng một cách tiếp cận khác, được gọi là thuật toán tiết kiệm. Từ đó thì sự quan tâm đến VRP đã được mở rộng từ một nhóm nhỏ các nhà toán học sang phạm vi rộng các nhà nghiên cứu và các nhà thực hành, từ các ngành khác nhau, trong nhiều lĩnh vực.
b. Đặc điểm của Vehicle Routing Problem trong toán học và nghiên cứu

Trước hết, Vehicle Routing Problem được đánh giá là một bài toán NP-hard (NP-khó). NP-hard là một dạng bài toán rất khó trong toán học. NP-hard (độ khó theo thời gian đa thức không xác định) là thuộc tính xác định của một loại bài toán không chính thức, có thể được hiểu "ít nhất là khó bằng các bài toán khó nhất trong NP".
P là viết tắt của chữ “polynomial”, tức là đa thức. Một vấn đề được xếp vào lớp P, nếu như có thuật toán sao cho cứ với mỗi “đầu vào” có chiều dài (tức là số chữ số hay ký hiệu để mô tả đầu vào) là N thì cho ra kết quả (đầu ra). P(N) là phép toán đơn giản nhất (ví dụ như cộng trừ hai số có một chữ số với nhau), trong đó P là một đa thức nào đó.
Có những vấn đề mà, việc tìm lời giải có thể mất rất nhiều thời gian, nhưng một khi có ai đó đưa ra lời giải, thì có thể kiểm tra trong một thời gian không quá lớn xem lời giải đó có đúng hay không. Ví dụ như các định lý hay các giả thuyết toán học: tìm ra định lý, chứng minh giả thuyết là công việc có thể vô cùng khó, nhưng một khi đã có chứng minh, thì việc kiểm tra chứng minh có đúng hay không là việc về nguyên tắc sẽ mất ít thời gian hơn nhiều so với việc tìm ra lời giải đúng.
c. Cách giải quyết bài toán Vehicle Routing Problem trong toán học và nghiên cứu

Nếu muốn thử sức với VRP, bạn có thể thực hiện theo cách sau:
Bài toán VRP truyền thống được đặt trong bối cảnh một công ty giao hàng. Trước hết, ta có một hoặc nhiều kho hàng, trong mỗi kho hàng là một đội xe giao hàng và một nhóm tài xế, và sẽ di chuyển trong hệ thống đường xá để đến được các điểm giao (khách hàng). Bài toán yêu cầu lời giải là một danh sách các tuyến đường, S, (mỗi tuyến đường cho mỗi xe, bắt đầu ở kho và kết thúc ở chính kho đó) sao cho tất cả yêu cầu của khách hàng và các điều kiện được thỏa mãn, bên cạnh đó chi phí vận tải cần được tối giản. Chi phí vận tải có thể là tiền, khoảng cách, thời gian,...
Hệ thống đường xá có thể được mô tả bằng đồ thị, trong đó các vòng cung là các con đường, còn các đỉnh là điểm giao giữa các con đường. Mỗi vòng cung có một chi phí đi kèm, thường thì chi phí chính là độ dài hoặc thời gian di chuyển và phụ thuộc vào từng loại phương tiện.
Muốn tính toán chi phí của mỗi tuyến đường, ta cần nắm rõ chi phí di chuyển và thời gian di chuyển giữa điểm giao và kho. Và để làm được điều này, ta có thể đặt các điểm giao và kho ở các đỉnh, và vòng cung là các con đường giữa chúng. Chi phí trên mỗi vòng cung là chi phí thấp nhất giữa hai điểm trên hệ thống đường xá ở đầu. Từ đây chúng ta có đồ thị hoàn chỉnh. Với mỗi cặp điểm i và j, tồn tại một vòng cung (i, j) mà chi phí là C, đây là chi phí thấp nhất để di chuyển từ i đến j. Thời gian di chuyển t là tổng thời gian di chuyển trên các vòng cung nối i và j.
Đôi khi bạn không thể đáp ứng tất cả các yêu cầu của khách hàng và trong những trường hợp đó, bạn có thể làm giảm một số nhu cầu của khách hàng hoặc không giao cho một số khách hàng.
3. Vehicle Routing Problem trong thực tiễn doanh nghiệp
a. Vì sao cần giải quyết Vehicle Routing Problem trong thực tiễn doanh nghiệp?

Đề bài gốc của bài toán VRP là: Làm thế nào để tạo ra một lộ trình tối ưu cho một đội xe giao hàng tới một lượng khách hàng có sẵn? Ngay từ đề bài, chúng ta đã thấy bài toán được đặt ra là dành cho doanh nghiệp.
Mục tiêu tối ưu của Vehicle Routing Problem cũng chính là mục tiêu mà doanh nghiệp muốn hướng tới với hoạt động logistics của mình. Thường hàm mục tiêu (Objectives) để tối ưu hướng đến 1 (không đồng thời) những mục tiêu sau:
- Giảm thiểu tổng quãng đường các xe di chuyển.
- Giảm thiểu tổng chi phí vận hành.
- Giảm thiểu tổng số lượng các xe được gán cho một ngày.
- Thời gian làm việc của các xe được gán đều nhau.
- Quãng đường di chuyển của các xe được gán đều nhau.
- Giảm thiểu số lượng đơn rớt.
Nói một cách khác, mục tiêu giải quyết bài toán Vehicle Routing Problem chính là đem lại lợi ích cho doanh nghiệp bằng cách giảm chi phí và tăng hiệu quả. Số liệu đã cho thấy trên thực tế, việc sử dụng các phần mềm tối ưu hóa trên máy tính để giải bài toán Vehicle Routing Problem có thể tiết kiệm 10% - 30% cho một công ty, do giao thông vận tải thường là một thành phần quan trọng trong giá thành sản phẩm (10%). Trên thực tế, chi phí logistics ở Việt Nam tương đương ~20% GDP. Do đó, bất kỳ khoản tiết kiệm nào do VRP tạo ra, thậm chí dưới 5%, đều đáng kể.

b. Vehicle Routing Problem trong thực tiễn doanh nghiệp là như thế nào?

Khác với hai ví dụ về nhân viên văn phòng và shipper giao bánh mì tôi đề cập ở trên, Vehicle Routing Problem trong thực tiễn doanh nghiệp là câu chuyện hoàn toàn khác. Lý do khiến bài toán này là một bài toán NP-hard, chính là do độ khó của nó khi mà ta càng đưa thêm nhiều điều kiện ràng buộc vào bài toán gốc. Khác với toán học, thực tiễn kinh doanh có vô số điều kiện mà ta cần giải quyết, ví dụ như tải trọng xe, thời gian nhận hàng, giao thông, đường cấm, trạm trung chuyển, nhiệt độ hàng,...
Bài toán Vehicle Routing Problem mà nhà sản xuất, nhà phân phối, nhà vận tải, 3PL, hay nhà bán lẻ gặp phải trong giao hàng có thể diễn đạt như sau:
Làm thế nào để tạo ra quãng đường tối ưu cho đội xe giao hàng bao gồm 12 xe tải và 8 xe máy tới 80 khách hàng với 150 đơn hàng? Trong đó:
- Mỗi xe có một tải trọng/thể tích chở hàng khác nhau, và cần phân chia đơn cho xe sao cho tải trọng/thể tích xe được tối ưu.
- Đơn hàng lạnh cần giao cho xe lạnh, đơn hàng thường cần giao cho xe thường.
- Đơn hàng lớn cần chia nhỏ để chia cho nhiều xe đến cùng một khách hàng.
- Xe máy nhận hàng ở trạm trung chuyển (cross-dock).
- Các cụm điểm giao của khách hàng A (một hệ thống siêu thị lớn) cần nhận hàng trước 6h00, một số khách hàng lẻ khác lại cần nhận hàng trong khoảng 10h - 12h, một số khác là 13h - 15h.
- Một số khách hàng tạp hóa trong ngõ nhỏ không thể nhận hàng bằng xe tải, và các khách hàng này nằm rải rác ở các quận khác nhau.
- Đường Lý Thường Kiệt và đường Trần Phú cấm tải từ 8h - 12h với xe tải tải trọng 1 tấn trở lên.
- Giờ tắc đường thường là 8h và 18h.
- Đội xe cần quay lại kho vào 19h để tập kết và trả hàng trả lại, chuẩn bị cho ngày giao tiếp theo với lượng đơn hàng khác.
- …
c. Các điều kiện ràng buộc trong vận tải/giao hàng ở Việt Nam
Khác với châu Âu, châu Mỹ hay Đông Á, khu vực Đông Nam Á hay Việt Nam nói riêng có những điều kiện ràng buộc rất riêng trong vận tải, giao hàng, ví dụ như giao hàng bằng xe máy, sử dụng kết hợp xe máy và xe tải, tắc đường, những con ngõ nhỏ, hay số lượng cửa hàng tạp hóa chiếm tỷ trọng lớn. Tuyến đường giao hàng tối ưu ở Việt Nam cần thỏa mãn cùng một lúc và phần lớn (càng nhiều càng tốt) các điều kiện ràng buộc sau:

Tuyến đường không chồng chéo: Tuyến đường chồng chéo sẽ dài hơn và thiếu hiệu quả hơn là tuyến đường không chồng chéo.

Khung thời gian làm việc: Tài xế, xe giao hàng đều có khung thời gian làm việc. Ta cần tạo ra lộ trình giao hàng nằm trong khung thời gian này.

Tối ưu hiệu quả (doanh thu): Khi số lượng đơn vượt khả năng chở của xe, mà không có thêm xe, hoặc điều kiện thời gian không cho phép, thì nên ưu tiên các đơn có giá trị từ cao đến thấp.

VRP với trọng lượng/thể tích hàng: Đơn hàng giao ở mỗi điểm giao có trọng lượng, thể tích khác nhau. Ta cần sắp xếp đơn hàng lên xe, làm sao để tải trọng/thể tích thùng xe được tối ưu nhất.
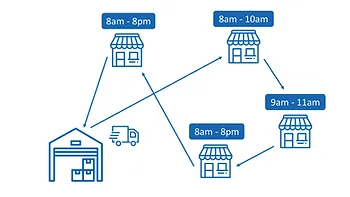 VRP với thời gian nhận hàng: Mỗi điểm giao có một khung thời gian nhận hàng khác nhau. Ta cần sắp xếp tuyến đường để thời gian đến mỗi điểm nằm trong khung thời gian của điểm giao đó.
VRP với thời gian nhận hàng: Mỗi điểm giao có một khung thời gian nhận hàng khác nhau. Ta cần sắp xếp tuyến đường để thời gian đến mỗi điểm nằm trong khung thời gian của điểm giao đó.
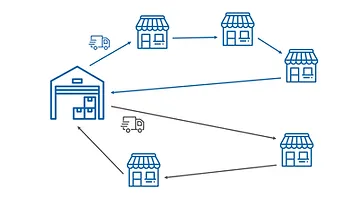
Tối ưu theo cụm: Nếu một điểm giao trong lộ trình của xe A nằm trong khu vực lộ trình của xe B (gần các điểm giao của B hơn A), thì điểm giao này sẽ được chuyển từ lộ trình của A sang B để làm tăng hiệu suất.
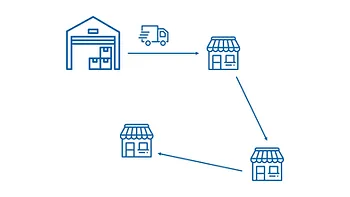
Vehicle Routing Problem mở: Cuối ngày, xe không cần quay lại kho (điểm xuất phát). Điều kiện này hữu dụng khi sử dụng những xe thuê ngoài: khi kết thúc lộ trình thì xe thuê ngoài không cần trở về kho để bàn giao giấy tờ hay hàng hoá. Mặt khác, bên thuê chở hàng sẽ chỉ cần trả tiền cho quãng đường mà xe di chuyển để chở hàng.
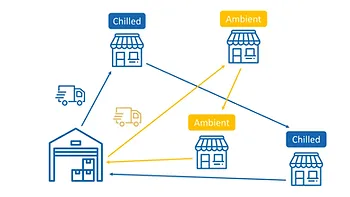
VRP cho giao hàng lạnh: Đối với doanh nghiệp sản xuất, phân phối thực phẩm, đồ uống, thuốc,... hay doanh nghiệp vận tải cung ứng lạnh, đây là một điều kiện hữu dụng. Đơn hàng lạnh (kem, thực phẩm đông lạnh) được thuật toán giao cho xe lạnh, đơn hàng mát (sữa, thuốc) giao cho xe mát, đơn hàng nhiệt độ thường giao cho xe thường.
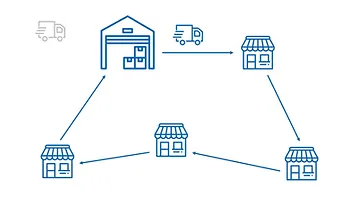
Giảm phương tiện giao hàng: Nếu có nhiều xe có lộ trình ngắn (kết thúc ngày sớm), thì ta có thể gộp các lộ trình này lại để giảm số lượng xe giao hàng, qua đó tiết kiệm chi phí.
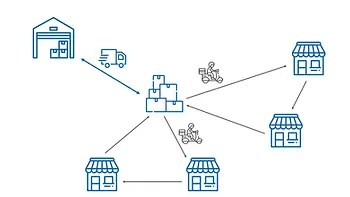
Mô hình Cross-dock (trạm trung chuyển): Xe tải lớn chở một lượng hàng lớn đến trạm trung chuyển. Sau đó các xe tải nhỏ, xe máy sẽ nhận hàng tại trạm trung chuyển để giao.
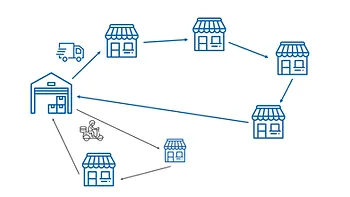 Điểm giao với yêu cầu phương tiện: Do điều kiện ngõ ngách, một số điểm giao chỉ có thể được giao bởi xe máy, xe tải tải trọng thấp,...
Điểm giao với yêu cầu phương tiện: Do điều kiện ngõ ngách, một số điểm giao chỉ có thể được giao bởi xe máy, xe tải tải trọng thấp,...
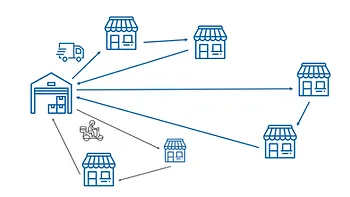
VRP với nhiều chuyến: Nếu vẫn còn đơn hàng và còn thời gian, xe có thể được giao thêm đơn để tối đa tổng khả năng làm việc của xe.
Đó đã phải là tất cả?
Trên đây là những điều kiện phần lớn công ty gặp phải trong giao hàng ở Việt Nam. Tất nhiên, đó chưa phải là tất cả điều kiện. Thực tế là mỗi doanh nghiệp lại có những đặc thù khác nhau, khiến cho số lượng điều kiện trong Vehicle Routing Problem có thể lên đến hàng chục, thậm chí hàng trăm. Abivin tự hào là đơn vị cung cấp giải pháp có thể giải quyết tất cả các điều kiện ràng buộc nêu trên, cộng thêm một số điều kiện khác không được đề cập đến trong tài liệu này.
4. Giải quyết Vehicle Routing Problem trong thực tiễn doanh nghiệp
a. Phương pháp thủ công
 Giải bài toán Vehicle Routing Problem (VRP) theo cách thủ công
Giải bài toán Vehicle Routing Problem (VRP) theo cách thủ công
Đây là cách làm giải quyết bài toán Vehicle Routing Problem ta thường thấy trong hoạt động Logistics truyền thống. Các công ty sẽ tuyển những Người điều phối có kinh nghiệm lâu năm, và dựa nhiều vào kinh nghiệm của những người điều phối này cho hoạt động giao hàng. Tất nhiên, nếu doanh nghiệp chỉ giao cho một lượng khách hàng cố định, với lượng đơn hàng cố định và đội xe cố định, hoặc doanh nghiệp không để tâm đến quá nhiều điều kiện như đề cập ở trên, thì doanh nghiệp hoàn toàn có thể hoạt động theo cách thủ công, dựa vào kinh nghiệm của người điều phối.
Cách làm thủ công này sẽ tiêu tốn của người điều phối khoảng 2 - 4 giờ đồng hồ mỗi ngày để lên lộ trình giao hàng. Tuy nhiên, doanh nghiệp có thể gặp rủi ro khi người điều phối vắng mặt và cần người thay thế, khiến việc đạt được kết quả tốt khi sắp xếp lộ trình thủ công gặp ảnh hưởng đáng kể.
b. Sử dụng công cụ giải toán miễn phí (free solver)
Có rất nhiều nhà nghiên cứu đã làm ra các công cụ giải bài toán Vehicle Routing Problem miễn phí. Bạn có thể tìm thấy dễ dàng trên internet. Dưới đây là một số công cụ như vậy:
- VRP Solver Softpedia:https://www.softpedia.com/get/Programming/Other-Programming-Files/VRP-solver.shtml
- VRP Solver Lehigh: https://coral.ise.lehigh.edu/larry/software/vrp-solver/
- VRP Solver Localsolver: https://www.localsolver.com/docs/last/exampletour/vrp.html
- VRP Solver Spreadsheet: https://vrp-spreadsheet-solver.windows10compatible.com/
Nhược điểm của cách làm này là mỗi công cụ chỉ có thể giải được khoảng 3 - 5 điều kiện. Bên cạnh đó là cách cài đặt phức tạp. Bạn có thể lập kế hoạch cho 10 - 50 điểm giao với cách này. Còn với 100 - 200 điểm, những công cụ trên sẽ mất từ hàng chục giờ đến hàng ngày để giải quyết xong bài toán.
c. Sử dụng phần mềm chuyên dụng
Ngày nay, có nhiều công ty cung cấp giải pháp tối ưu tuyến đường bằng cách giải bài toán Vehicle Routing Problem. Đây cũng chính là cách hiệu quả nhất để giải bài toán này cho doanh nghiệp.
Điểm khác biệt của phần mềm tối ưu hóa tuyến đường so với các phần mềm quản lý đội xe nằm ở thuật toán tối ưu tự động. Chỉ cần upload dữ liệu bạn có và phần mềm sẽ tự động đưa ra lộ trình giao hàng tối ưu nhất cho xe, chỉ sau vài giây, vài phút xử lý dữ liệu. Đây cũng chính là vài phút mà phần mềm cần để giải quyết hàng loạt điều kiện như đề cập ở trên.
Nếu bạn là người lập kế hoạch vận tải, sự trợ giúp của phần mềm không chỉ giúp bạn tiết kiệm thời gian cho bản thân mà còn đảm bảo 100% tính chính xác trong quá trình xử lý dữ liệu, khắc phục hoàn toàn những sai sót thường gặp khi tính toán thủ công. Bên cạnh đó, bạn có thể đảm bảo chính xác quy trình hoạt động, giảm chi phí cho doanh nghiệp, cũng như tạo ra lộ trình phù hợp cho nhóm tài xế.
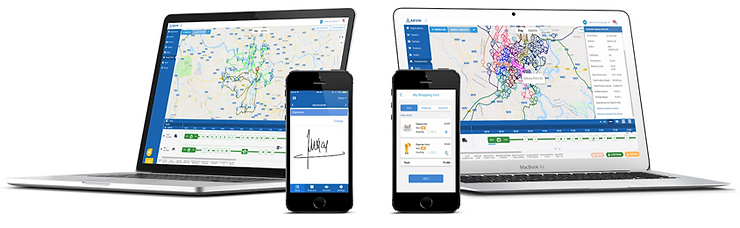
Giải bài toán Vehicle Routing Problem (VRP) bằng phần mềm
Phần mềm tối ưu hóa tuyến đường tự động xuất ra một bản đồ hướng dẫn đường đi chi tiết và dễ nhìn. Trong trường hợp bạn cần thay đổi thông số cho phù hợp với nhu cầu phát sinh, phần mềm sẽ đưa ra ngay lập tức một lộ trình thay thế tối ưu theo đúng những thay đổi của bạn.
Dù là một chuyên gia đầy kinh nghiệm hay chỉ một người mới bước chân vào ngành logistics, việc dự đoán những phát sinh ngoài ý muốn và thay đổi kế hoạch nhanh chóng theo nhu cầu tức thời của vận chuyển chưa bao giờ là một nhiệm vụ dễ dàng. Tuy nhiên, với sự trợ giúp của phần mềm tối ưu hóa tuyến đường, việc thay đổi hay tối ưu lại lộ trình chỉ diễn ra trong vài click chuột. Đặc biệt hơn cả là bạn có thể tiết kiệm đáng kể chi phí logistics. Bên cạnh đó, khi công việc tinh toán nặng nhọc được dành cho máy tính, bạn có thể dùng hàng giờ tiết kiệm được vào việc quản lý, theo dõi đội xe và cải thiện hiệu quả công việc.
Lời kết
Logistics chưa bao giờ là một công việc dễ dàng. Trên thực tế, Vehicle Routing Problem chỉ là một trong số rất nhiều bài toán trong logistics. Mặc dù vậy, việc giải quyết thành công bài toán này có thể giúp tiết kiệm từ 10 - 30% chi phí cho hoạt động vận tải của doanh nghiệp bạn. Nhiều khách hàng của Abivin đã ghi nhận mức lợi tức đầu từ (ROI) lên đến ~200% trong 3 năm triển khai phần mềm tối ưu tuyến đường.
Doanh nghiệp của bạn có đang gặp vấn đề giao hàng với năng suất thấp, quá phụ thuộc vào con người trong điều phối, kế hoạch giao hàng thiếu hiệu quả dẫn đến chi phí cao? Abivin sẵn sàng lắng nghe những vấn đề mà bạn đang gặp phải để đưa ra lời giải tối ưu, giúp mỗi chuyến giao hàng không còn là nỗi lo âu của bạn.
Vehicle Routing Problem (VRP) Là Gì?